7 algoritmen die elke programmeur zou moeten kennen

Als student programmeren heb je in de loop van je carrière waarschijnlijk veel verschillende algoritmen geleerd. Vaardig worden in verschillende algoritmen is absoluut essentieel voor elke programmeur.

Met zoveel algoritmen kan het een uitdaging zijn om bij te houden wat essentieel is. Als je je voorbereidt op een sollicitatiegesprek of gewoon je vaardigheden wilt opfrissen, zal deze lijst het relatief eenvoudig maken. Lees verder terwijl we de meest essentiële algoritmen voor programmeurs opsommen.

1. Dijkstra's algoritme

Edsger Dijkstra was een van de meest invloedrijke computerwetenschappers van zijn tijd, en hij heeft bijgedragen aan: veel verschillende gebieden van informatica, waaronder besturingssystemen, compilerconstructie en nog veel meer meer. Een van Dijkstra's meest opvallende bijdragen is de vindingrijkheid van zijn kortste pad-algoritme voor grafieken, ook wel bekend als Dijkstra's Shortest Path Algorithm.

Dijkstra's algoritme vindt het enige kortste pad in een graaf van een bron naar alle graafhoekpunten. Bij elke iteratie van het algoritme wordt een hoekpunt toegevoegd met de minimale afstand tot de bron en een hoekpunt dat niet bestaat in het huidige kortste pad. Dit is de hebzuchtige eigenschap die wordt gebruikt door het algoritme van Djikstra.

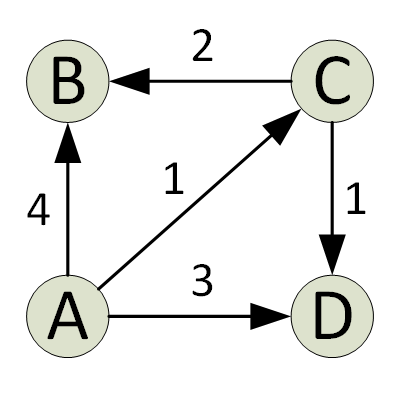
Het algoritme wordt typisch geïmplementeerd met behulp van een set. Dijkstra's algoritme is zeer efficiënt wanneer geïmplementeerd met een Min Heap; je kunt het kortste pad vinden in slechts O(V+ElogV) tijd (V is het aantal hoekpunten en E is het aantal randen in een gegeven grafiek).

Dijkstra's algoritme heeft zijn beperkingen; het werkt alleen op gerichte en ongerichte grafieken met randen van positief gewicht. Voor negatieve gewichten heeft het Bellman-Ford-algoritme doorgaans de voorkeur.

Interviewvragen bevatten vaak het algoritme van Djikstra, dus we raden ten zeerste aan om de ingewikkelde details en toepassingen ervan te begrijpen.

2. Sorteren samenvoegen

We hebben een aantal sorteeralgoritmen in deze lijst en merge sort is een van de belangrijkste algoritmen. Het is een efficiënt sorteeralgoritme gebaseerd op de programmeertechniek Divide and Conquer. In het ergste geval kan merge sort "n" getallen sorteren in slechts O(nlogn) tijd. Vergeleken met primitieve sorteertechnieken zoals: Bellen sorteren (dat kost O (n ^ 2) tijd), merge sort is uitstekend efficiënt.

Verwant: Inleiding tot het samenvoegen van sorteeralgoritmen

Bij merge sort wordt de te sorteren array herhaaldelijk opgesplitst in subarrays totdat elke subarray uit één enkel getal bestaat. Het recursieve algoritme voegt vervolgens herhaaldelijk de subarrays samen en sorteert de array.

3. Snel sorteren

Quicksort is een ander sorteeralgoritme dat is gebaseerd op de programmeertechniek Divide and Conquer. In dit algoritme wordt eerst een element gekozen als de spil, en de hele array wordt vervolgens rond deze spil verdeeld.

Zoals je waarschijnlijk al geraden hebt, is een goede spil cruciaal voor een efficiënte sortering. De spil kan een willekeurig element, het media-element, het eerste element of zelfs het laatste element zijn.

Implementaties van quicksort verschillen vaak in de manier waarop ze een pivot kiezen. In het gemiddelde geval sorteert quicksort een grote array met een goede spil in slechts O (nlogn) tijd.

De algemene pseudocode van quicksort verdeelt herhaaldelijk de array op de spil en positioneert deze in de juiste positie van de subarray. Het plaatst ook de elementen die kleiner zijn dan de spil aan de linkerkant en de elementen die groter zijn dan de spil aan de rechterkant.

4. Diepte Eerste zoekopdracht

Depth First Search (DFS) is een van de eerste grafische algoritmen die aan studenten wordt geleerd. DFS is een efficiënt algoritme dat wordt gebruikt om een ​​grafiek te doorzoeken of te doorzoeken. Het kan ook worden aangepast om te worden gebruikt bij het doorkruisen van bomen.

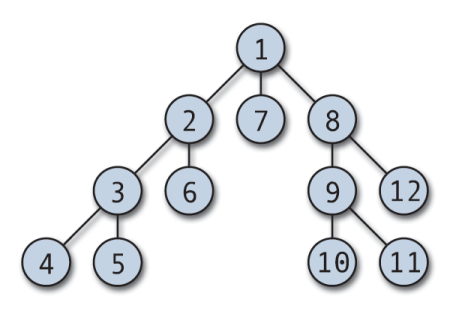
De DFS-traversal kan starten vanaf elk willekeurig knooppunt en duikt in elk aangrenzend hoekpunt. Het algoritme keert terug als er geen onbezocht hoekpunt is, of als er een doodlopende weg is. DFS wordt meestal geïmplementeerd met een stapel en een booleaanse array om de bezochte knooppunten bij te houden. DFS is eenvoudig te implementeren en buitengewoon efficiënt; het werkt (V+E), waarbij V het aantal hoekpunten is en E het aantal randen.

Typische toepassingen van de DFS-traversal zijn onder meer topologische sortering, het detecteren van cycli in een grafiek, pathfinding en het vinden van sterk verbonden componenten.

5. Breedte-eerst zoeken

Breadth-First Search (BFS) is ook bekend als een niveauvolgorde voor bomen. BFS werkt in O(V+E) vergelijkbaar met een DFS-algoritme. BFS gebruikt echter een wachtrij in plaats van de stapel. DFS duikt in de grafiek, terwijl BFS de grafiek in de breedte doorloopt.

Het BFS-algoritme gebruikt een wachtrij om de hoekpunten bij te houden. Niet-bezochte aangrenzende hoekpunten worden bezocht, gemarkeerd en in de wachtrij geplaatst. Als het hoekpunt geen aangrenzend hoekpunt heeft, wordt een hoekpunt uit de wachtrij verwijderd en verkend.

BFS wordt vaak gebruikt in peer-to-peer-netwerken, het kortste pad van een ongewogen grafiek en om de minimale opspannende boom te vinden.

6. Binaire zoekopdracht

Binaire zoekopdracht is een eenvoudig algoritme om het vereiste element in een gesorteerde array te vinden. Het werkt door de array herhaaldelijk in tweeën te delen. Als het gewenste element kleiner is dan het middelste element, dan wordt de linkerkant van het middelste element verder verwerkt; anders wordt de rechterkant gehalveerd en opnieuw gezocht. Het proces wordt herhaald totdat het gewenste element is gevonden.

De slechtste tijdscomplexiteit van binair zoeken is O(logn), wat het zeer efficiënt maakt bij het zoeken naar lineaire arrays.

7. Minimale overspannende boomalgoritmen

Een minimale opspannende boom (MST) van een graaf heeft de minimale kosten van alle mogelijke opspannende bomen. De kosten van een opspannende boom zijn afhankelijk van het gewicht van de randen. Het is belangrijk op te merken dat er meer dan één minimale opspannende boom kan zijn. Er zijn twee belangrijke MST-algoritmen, namelijk die van Kruskal en Prim.

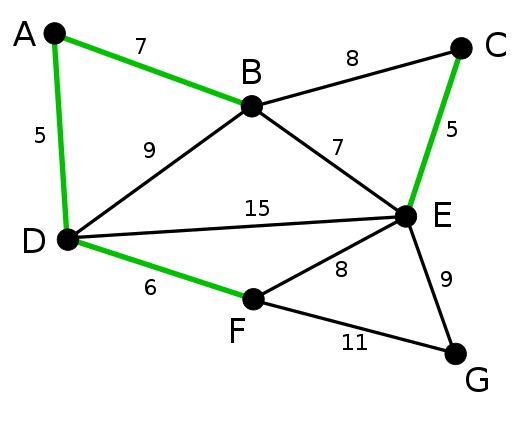
Het algoritme van Kruskal creëert de MST door de edge met minimale kosten toe te voegen aan een groeiende set. Het algoritme sorteert eerst randen op hun gewicht en voegt vervolgens randen toe aan de MST vanaf het minimum.

Het is belangrijk op te merken dat het algoritme geen randen toevoegt die een cyclus vormen. Het algoritme van Kruskal heeft de voorkeur voor schaarse grafieken.

Het algoritme van Prim gebruikt ook een hebzuchtige eigenschap en is ideaal voor dichte grafieken. Het centrale idee in Prim's MST is om twee verschillende sets hoekpunten te hebben; de ene set bevat de groeiende MST, terwijl de andere ongebruikte hoekpunten bevat. Bij elke iteratie wordt de minimale gewichtsrand geselecteerd die de twee sets verbindt.

Minimale spanning tree-algoritmen zijn essentieel voor clusteranalyse, taxonomie en uitzendnetwerken.

Een efficiënte programmeur is bekwaam met algoritmen

Programmeurs leren en ontwikkelen voortdurend hun vaardigheden, en er zijn enkele essentiële zaken die iedereen moet beheersen. Een ervaren programmeur kent de verschillende algoritmen, de voor- en nadelen van elk en welk algoritme het meest geschikt is voor een bepaald scenario.

Een inleiding tot het Shell Sort Algoritme

Hoewel het sorteren van schelpen niet de meest efficiënte methode is, hebben beginners veel te winnen bij het oefenen ervan.

Lees volgende

Over de auteur